Fractal dimension of the large-scale structure
Posted: March 13 2010
A fundamental feature of the large-scale structure is the scale where the distribution becomes homogeneous (as is expected in cosmological models based on inflation). It's interesting that there seems to be a significant discrepancy in this feature between [tex]\Lambda[/tex]CDM N-body simulations and observations.
A simple tool for studying the homogeneity is the fractal dimension of the point set of galaxies (or N-body simulation particles). You take an occupied point and draw a sphere of radius R around it. As you vary [tex]R[/tex], the number of points inside the sphere changes as [tex]N(R)=A R^{-D(R)}[/tex], where A is a constant. Do this for all occupied points, and take the average. The resulting [tex]D(R)[/tex] is the fractal dimension of the point set. If the distribution is homogeneous above a scale [tex]L[/tex], then [tex]D=3[/tex], in three space dimensions.
The first set of observations where one can see the transition to homogeneity is SDSS. The LRG sample gives the following plot (from arXiv:astro-ph/0411197):
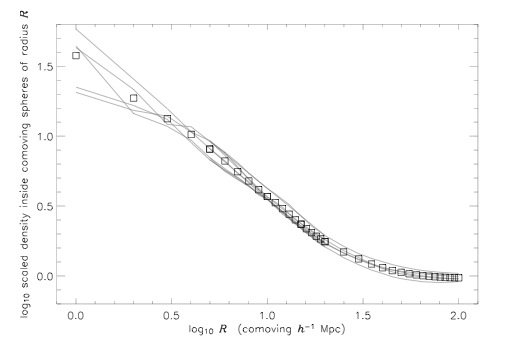
The plot shows (essentially) log(N) as a function of log(R), with a convention where they use [tex]D-3[/tex] instead of [tex]D[/tex], so 0 corresponds to homogeneity.
In the plot we see a transition to homogeneity around 70-100 [tex]h^{-1}[/tex]Mpc. There is criticism of whether homogeneity has really been established, since the number of independent spheres at large radii is rather small, and there are large fluctuations on large scales. See arXiv:astro-ph/0610938, 0805.1132, 0812.3260, 0902.0229 and 0909.0132. See 0910.3833 or 0912.1191 for a short summary.
Such concerns aside, even if the observed homogeneity scale is really 100 Mpc, simulations look very different. Witness the comparison (from arXiv:astro-ph/0501583):
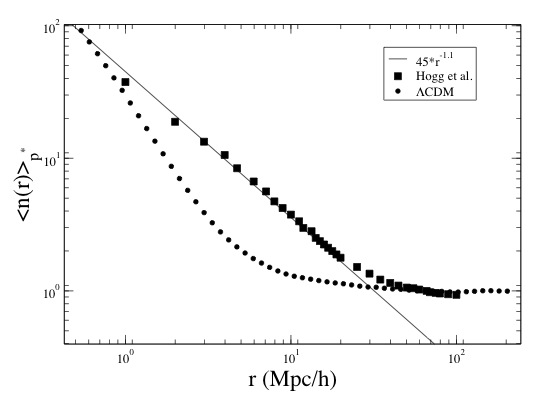
The simulated distribution reaches homogeneity cleanly around 10 [tex]h^{-1}[/tex]Mpc, an order of magnitude earlier than the observed one. In fact the distributions are different on all scales from 1 to 70 [tex]h^{-1}[/tex]Mpc or so. In addition, the probability density function of density fluctuations is nicely Gaussian on scales above 10 [tex]h^{-1}[/tex]Mpc in the simulations, whereas this is not true for the observations. (See the above quoted papers for details.)
There is also a reported discrepancy in the numbers of luminous superclusters, with many more observed than produced in the simulations, see arXiv:astro-ph/0603764, arXiv:astro-ph/0604539 and arXiv:astro-ph/0605393. (I wish this work would be independently checked by other groups.)
An interesting question is what is the reason for this difference. We observe the baryons but simulate dark matter, but I find it difficult to see how bias could explain such a large discrepancy on such large scales. (Admittedly, I know little about biasing.) Two possibilities which come immediately to mind are changes in the initial power spectrum on large scales (to produce more structure) or in the expansion history (ditto). (My favourite candidate is the influence of non-Newtonian aspects of general relativity, which are missing from the simulations, but that's another story.)
A simple tool for studying the homogeneity is the fractal dimension of the point set of galaxies (or N-body simulation particles). You take an occupied point and draw a sphere of radius R around it. As you vary [tex]R[/tex], the number of points inside the sphere changes as [tex]N(R)=A R^{-D(R)}[/tex], where A is a constant. Do this for all occupied points, and take the average. The resulting [tex]D(R)[/tex] is the fractal dimension of the point set. If the distribution is homogeneous above a scale [tex]L[/tex], then [tex]D=3[/tex], in three space dimensions.
The first set of observations where one can see the transition to homogeneity is SDSS. The LRG sample gives the following plot (from arXiv:astro-ph/0411197):

The plot shows (essentially) log(N) as a function of log(R), with a convention where they use [tex]D-3[/tex] instead of [tex]D[/tex], so 0 corresponds to homogeneity.
In the plot we see a transition to homogeneity around 70-100 [tex]h^{-1}[/tex]Mpc. There is criticism of whether homogeneity has really been established, since the number of independent spheres at large radii is rather small, and there are large fluctuations on large scales. See arXiv:astro-ph/0610938, 0805.1132, 0812.3260, 0902.0229 and 0909.0132. See 0910.3833 or 0912.1191 for a short summary.
Such concerns aside, even if the observed homogeneity scale is really 100 Mpc, simulations look very different. Witness the comparison (from arXiv:astro-ph/0501583):

The simulated distribution reaches homogeneity cleanly around 10 [tex]h^{-1}[/tex]Mpc, an order of magnitude earlier than the observed one. In fact the distributions are different on all scales from 1 to 70 [tex]h^{-1}[/tex]Mpc or so. In addition, the probability density function of density fluctuations is nicely Gaussian on scales above 10 [tex]h^{-1}[/tex]Mpc in the simulations, whereas this is not true for the observations. (See the above quoted papers for details.)
There is also a reported discrepancy in the numbers of luminous superclusters, with many more observed than produced in the simulations, see arXiv:astro-ph/0603764, arXiv:astro-ph/0604539 and arXiv:astro-ph/0605393. (I wish this work would be independently checked by other groups.)
An interesting question is what is the reason for this difference. We observe the baryons but simulate dark matter, but I find it difficult to see how bias could explain such a large discrepancy on such large scales. (Admittedly, I know little about biasing.) Two possibilities which come immediately to mind are changes in the initial power spectrum on large scales (to produce more structure) or in the expansion history (ditto). (My favourite candidate is the influence of non-Newtonian aspects of general relativity, which are missing from the simulations, but that's another story.)