CAMB: k-independent growth factor / large scale effects
-
Sebastian Bocquet
- Posts: 3
- Joined: February 21 2012
- Affiliation: USM Munich
CAMB: k-independent growth factor / large scale effects
I am currently working on a formalism that yields a growth factor which is a function of redshift only (no k-dependence).
This works fine on small scales (high k), where the growth factor indeed is nearly independent of k; however, it fails to match CAMB's predictions on very large scales >Gpc. I guess this is due to the crossing of the Hubble scale which suppresses the growth of structure.
My question is:
Where and how does CAMB account for this effect?
Any good reference as for formulae?
Many thanks!
This works fine on small scales (high k), where the growth factor indeed is nearly independent of k; however, it fails to match CAMB's predictions on very large scales >Gpc. I guess this is due to the crossing of the Hubble scale which suppresses the growth of structure.
My question is:
Where and how does CAMB account for this effect?
Any good reference as for formulae?
Many thanks!
-
Antony Lewis
- Posts: 1943
- Joined: September 23 2004
- Affiliation: University of Sussex
- Contact:
Re: CAMB: k-independent growth factor / large scale effects
CAMB evolves the full linear perturbation theory equations.
The synchonous-gauge total matter density perturbation should grow in a k-independent way in most models on large scales (though the Newtonian gauge density perturbation will change due to the horizon scale - see eg. 1105.5292).
The synchonous-gauge total matter density perturbation should grow in a k-independent way in most models on large scales (though the Newtonian gauge density perturbation will change due to the horizon scale - see eg. 1105.5292).
-
Sebastian Bocquet
- Posts: 3
- Joined: February 21 2012
- Affiliation: USM Munich
CAMB: k-independent growth factor / large scale effects
Thanks Antony for that quick reply.
I know that CAMB evolves the full equations; I am trying to understand the evolution as a scale independent growth factor.
I plotted powerspectra at different redshifts ("normalised" at low k) and am now wondering about this k-dependence.
ps_z_evo.ps
Could you please help me understanding this behaviour?
Many thanks!
I know that CAMB evolves the full equations; I am trying to understand the evolution as a scale independent growth factor.
I plotted powerspectra at different redshifts ("normalised" at low k) and am now wondering about this k-dependence.
ps_z_evo.ps
Could you please help me understanding this behaviour?
Many thanks!
-
Antony Lewis
- Posts: 1943
- Joined: September 23 2004
- Affiliation: University of Sussex
- Contact:
Re: CAMB: k-independent growth factor / large scale effects
As far as I can see this is a physical effect. I think the synchronous-gauge total density perturbation only grows in a scale-independent way to the extent that pressureless matter dominates the perurbation densities, the total density is comoving with the CDM, the contribution of decaying modes is negligible (or at least their contribution is scale independent), and the baryons are uninteracting.
Just at the moment I can't put my finger on a single effect that simply explains what you see, but the effect is significantly smaller on the largest-scales if you plot the power spectrum of the total comoving density perturbation rather than the default synchonous (CDM-comoving) one.
Just at the moment I can't put my finger on a single effect that simply explains what you see, but the effect is significantly smaller on the largest-scales if you plot the power spectrum of the total comoving density perturbation rather than the default synchonous (CDM-comoving) one.
-
Sebastian Bocquet
- Posts: 3
- Joined: February 21 2012
- Affiliation: USM Munich
CAMB: k-independent growth factor / large scale effects
Thanks again!
What is the easiest way then to obtain the power spectrum of the total comoving density perturbation from CAMB? Are both (synchronous and Newtonian) just related by
\Delta_N^i=\Delta^i - 3H\sigma/k
so that I only have to sum over CDM and dark energy for low redshifts and add the 3H\sigma/k term to my results?
What is the easiest way then to obtain the power spectrum of the total comoving density perturbation from CAMB? Are both (synchronous and Newtonian) just related by
\Delta_N^i=\Delta^i - 3H\sigma/k
so that I only have to sum over CDM and dark energy for low redshifts and add the 3H\sigma/k term to my results?
-
Antony Lewis
- Posts: 1943
- Joined: September 23 2004
- Affiliation: University of Sussex
- Contact:
Re: CAMB: k-independent growth factor / large scale effects
For the record here are some plots of the synchronous-gauge total-matter growth rate at some different large scales:
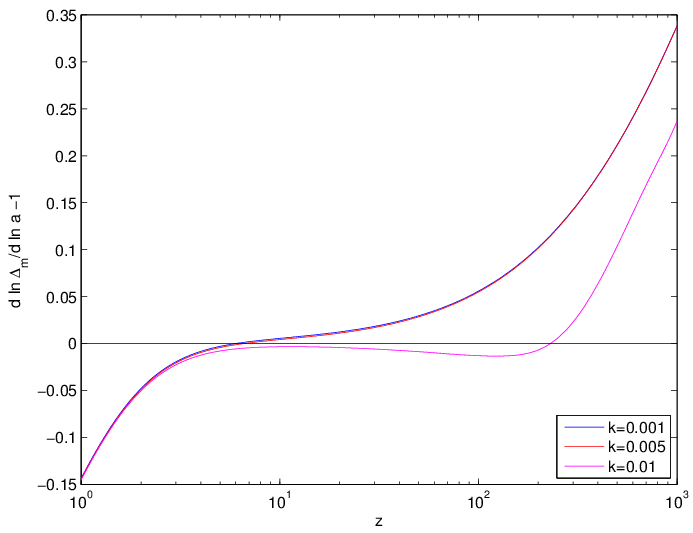

(the naive matter dominated result would give 0 on the left axis).
I've not checked the analytics, but would guess the physical picture for the main effect is that while adiabatic modes are outside the horizon [tex]\Delta_m = 3\Delta_R/4[/tex]. At relatively high redshift the radiation density contributes significantly, setting up faster infall velocity than if [tex]\Omega_R=0[/tex] (R=radiation). When the mode enters the horizon, [tex]\Delta_R[/tex] falls to nearly 0 due to free-streaming of the radiation, and the growth rate slows slightly compared to a similar mode still outside the horizon. Larger modes will have higher growth rate, and this velocity difference will persist (redshifting [tex]\propto 1/a[/tex], and hence corresponding to a decaying mode) some time after the mode enters the horizon, giving scale-dependent growth rate until the velocity differences have redshifted to being negligible.
Modes that enter the horizon after matter radiation equality correspond to relatively low perturbation amplitudes and small effects can be relatively more important.


(the naive matter dominated result would give 0 on the left axis).
I've not checked the analytics, but would guess the physical picture for the main effect is that while adiabatic modes are outside the horizon [tex]\Delta_m = 3\Delta_R/4[/tex]. At relatively high redshift the radiation density contributes significantly, setting up faster infall velocity than if [tex]\Omega_R=0[/tex] (R=radiation). When the mode enters the horizon, [tex]\Delta_R[/tex] falls to nearly 0 due to free-streaming of the radiation, and the growth rate slows slightly compared to a similar mode still outside the horizon. Larger modes will have higher growth rate, and this velocity difference will persist (redshifting [tex]\propto 1/a[/tex], and hence corresponding to a decaying mode) some time after the mode enters the horizon, giving scale-dependent growth rate until the velocity differences have redshifted to being negligible.
Modes that enter the horizon after matter radiation equality correspond to relatively low perturbation amplitudes and small effects can be relatively more important.